二项分布与超几何分布
在高考概率题型中,二项分布和超几何分布是两个非常重要的概率模型,它们在解决实际问题中发挥着关键作用。其中,二项分布描述的是固定次数的独立实验中,成功的次数的概率分布。而超几何分布则描述的是不返回抽样问题,即从有限的总体中抽取一定数量的样本时,其中含有特定种类的数量的概率分布。在解题过程中,正确地区分题目条件是否涉及到放回或不放回抽样是解决超几何分布和二项分布问题的关键。掌握这两个分布的定义、性质和计算方法,对于提高学生的逻辑思维能力和解决复杂问题的能力具有重要意义。这也是高中数学教育中强调概率统计部分的原因之一。
要点梳理
一、n次独立重复试验
在相同条件下重复做的n次试验称为n次独立重复试验.
特点:
1.各次之间相互独立;
2.每一次试验只有两种结果,即要么发生,要么不发生; 每一次试验中各事件发生的概率都是一样的.
二、二项分布

三、超几何分布
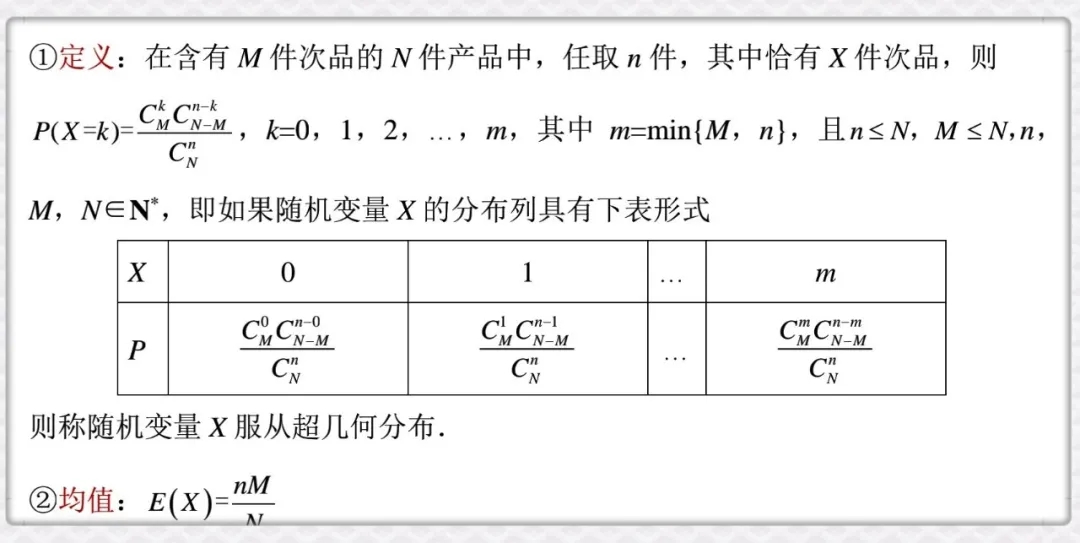
四、二项分布和超几何分布区别和联系
1. 二项分布是放回抽样问题,在每次试验中某一事件发生的概率是相同的,而超几何分布是不放回抽样问题,在每次试验中某一事件发生的概率是不相同的。
2. 二项分布不需要知道总体的容量,而超几何分布需要知道总体的容量;
3. 当总体的容量非常大时,超几何分布近似于二项分布。
共有哪些考点呢?
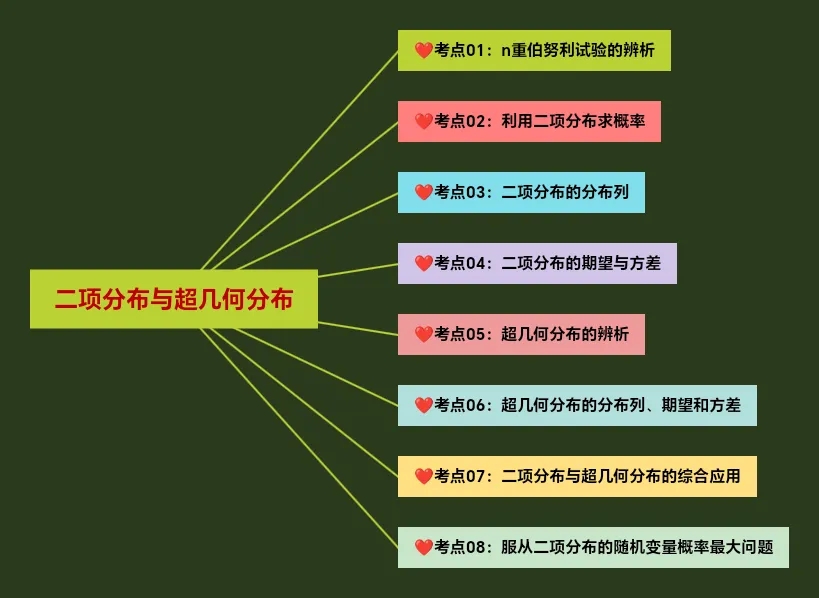
考点一:n重伯努利试验的辨析



考点二:利用二项分布求概率


考点三:二项分布的分布列





考点四:二项分布的期望与方差


考点五:超几何分布的辨析




考点六:超几何分布的分布列、期望和方差



考点七:二项分布与超几何分布的综合应用





考点八:服从二项分布的随机变量概率最大问题




-1.gif)