经常有学生问二项分布与超几何分布到底怎么区分,是利用二项分布的公式去解决这道概率题目,还是利用超几何分布公式解决呢?
好多学生查阅参考书寻找答案,其实这个问题的回答就出现在教材上, 北师大版新课标教材选修2-3从两个方面给出了很好的解释.
一 、两者的定义是不同的
教材中的定义:
1、超几何分布


2、独立重复试验与二项分布

本质区别:
(1) 超几何分布描述的是不放回抽样问题,而二项分布描述的是放回抽样问题.
(2) 超几何分布中的概率计算实质上是古典概型问题;二项分布中的概率计算实质上是相互独立事件的概率问题.
二、两者之间是有联系的



从以上分析可以看出两者之间的联系:当调查研究的样本容量非常大时,在有放回地抽取与无放回地抽取条件下,计算得到的概率非常接近,可以近似把超几何分布认为是二项分布.
下面看相关例题
例1.(2016·漯河模拟)寒假期间,我市某校学生会组织部分同学,用“10分制”随机调查“阳光花园”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶),若幸福度分数不低于8.5分,则称该人的幸福度为“幸福”.

注:先不要急于看答案,大家先自己解一下这道题再往下看,会有意想不到的收获哦!

[错解分析]第二问的选人问题是不放回抽样问题, 按照定义先考虑超几何分布,但是题目中又明确给出:“以这16人的样本数据来估计整个社区的总体数据,从该社区(人数很多)任选3人”,说明不是从16人中任选3人,而是从该社区(人数很多)任选3人,所以可以近似看作是3次独立重复试验,应该按照二项分布去求解,而不能按照超几何分布去处理.

柳暗花明又一村
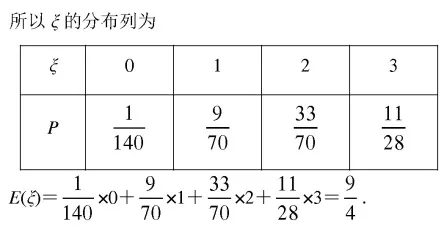
从以上解题过程中我们还发现,错解中的期望值与正解中的期望值相等,好多学生都觉得不可思议,怎么会出现相同的结果呢?其实这还是由于前面解释过的原因,超几何分布与二项分布是有联系的,看它们的期望公式:

总结
综上可知,当提问中涉及“用样本数据来估计总体数据”字样的为二项分布。
高考解题中,我们还是要分清超几何分布与二项分布的区别,以便能正确的解题,拿到满分!
-1.gif)